LCM of 12, 15 and 21: How to find LCM of 12, 15 and 21?

The LCM of 12, 15 and 21 is 420. Least Common Multiple (LCM) of a set of numbers is the smallest number that all of them can multiply into. In this blog, we’ll explain simple ways to find the LCM of 12, 15, and 21.

Here are three easy methods to find the LCM of 12, 15, and 21:

1. Prime Factorization Method

Break each number into its prime factors and use the highest power of each factor.

• 12 = 2 × 2 × 3 (or 2² × 3)
• 15 = 3 × 5
• 21 = 3 × 7
• Taking the highest powers: 2² × 3 × 5 × 7 = 420

Thus, LCM(12, 15, 21) = 420.

2. Listing Multiples Method

List the multiples of each number and find the smallest one they all share.

• Multiples of 12: 12, 24, 36, 48, 60, ..., 420, ...
• Multiples of 15: 15, 30, 45, 60, ..., 420, ...
• Multiples of 21: 21, 42, 63, ..., 420, ...
• The smallest common multiple is 420.

Thus, LCM(12, 15, 21) = 420.

3. Division Method

Divide all numbers by common factors until you reach 1.

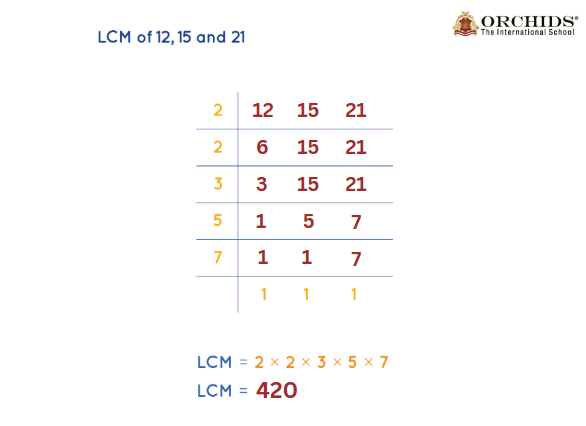
1. Divide 12, 15, and 21 by 3 → (4, 5, 7)
2. 4, 5 and 7 all are divisible by 1 only
3. Multiply the divisors: 3 × 4 × 5 × 7 = 420

Thus, LCM(12, 15, 21) = 420.

Conclusion

The LCM of 12, 15, and 21 is 420, and you can find it using prime factorization, listing multiples, or division.