LCM of 336 and 54: How to find LCM of 336 and 54?

The LCM of 336 and 54 is 3024. Least Common Multiple (LCM) of two numbers is the smallest number that is a multiple of both. The LCM of 336 and 54 is the smallest number that both 336 and 54 fit into. In this blog, we’ll explain easy ways to find the LCM of 336 and 54.

How to Find the LCM of 336 and 54

Here are three simple methods to find the LCM of 336 and 54:

1. Prime Factorization Method

We break each number into its prime factors and take the highest power of each factor.

• 336 = 2 × 2 × 2 × 2 × 3 × 7
• 54 = 2 × 3 × 3 × 3
• Taking the highest powers: 2⁴ × 3³ × 7 = 3024

Thus, LCM(336,54) = 3024.

2. Listing Multiples Method

We list the multiples of both numbers and find the smallest one they share.

• Multiples of 336: 336, 672, 1008, 1344, 1680, 2016, 2352, 2688, 3024, ...
• Multiples of 54: 54, 108, 162, 216, 270, 324, ..., 3024, ...
• The smallest common multiple is 3024.

Thus, LCM(336,54) = 3024.

3. Division Method

We divide both numbers by their common factors until we get 1.

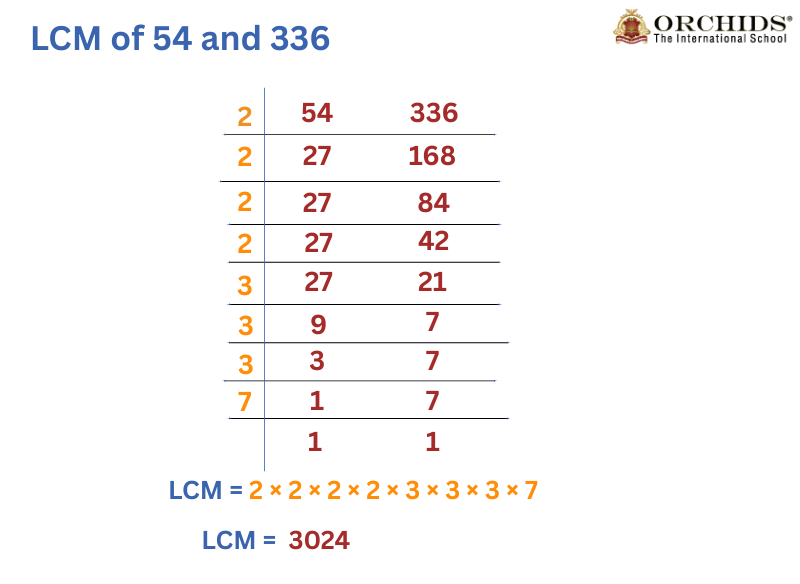
1. Divide 336 and 54 by 2 → (168, 27)
2. Divide 168 and 27 by 3 → (56, 9)
3. Both 56 and 9 are divisible only by 1.
4. Multiply the divisors: 2 × 3 × 56 × 9 = 3024

Thus, LCM(336,54) = 3024.

Conclusion

The LCM of 336 and 54 is 3024, and you can find it using prime factorization, listing multiples, or division. These methods make LCM calculations simple and useful.