LCM of 4 and 6: How to find LCM of 4 and 6?

The LCM of 4 and 6 is 12. Least Common Multiple (LCM) of two numbers is the smallest number that is evenly divisible by both numbers. The LCM of 4 and 6 is the smallest number that is a multiple of both 4 and 6. In this blog, we will explore different methods to calculate the LCM of 4 and 6.

Methods to Find the LCM of 4 and 6

There are multiple ways to calculate the LCM of 4 and 6. Let’s look at the most common methods:

1. Prime Factorization Method

In this method, we find the prime factors of each number and multiply the highest powers of all prime factors.

• Prime factorization of 4: 2 × 2
• Prime factorization of 6: 2 × 3
• Taking the highest powers of all prime factors: 2² × 3 = 12

Thus, LCM(4,6) = 12

2. Listing Multiples Method

We list the multiples of both numbers and find the smallest common multiple.

• Multiples of 4: 4, 8, 12, 16, 20, 24, ...
• Multiples of 6: 6, 12, 18, 24, 30, ...
• The smallest common multiple is 12

Thus, LCM(4,6) = 12

3. Division Method

In this method, we divide both numbers by their common prime factors until we get 1.

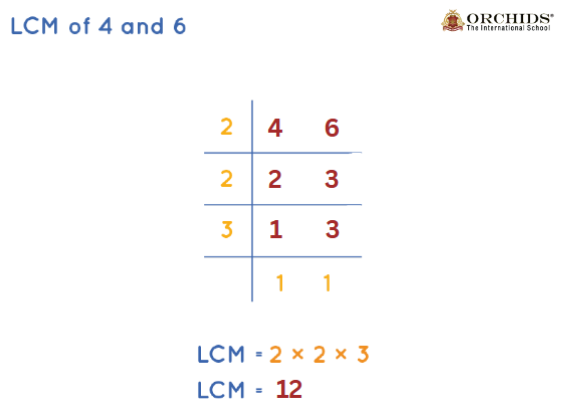
1. Divide 4 and 6 by 2 → (2, 3)
2. 2 and 3 are only divisible by 1. So, the divisors are 2, 3, 2.
3. Multiply all divisors: 2 x 2 x 3 = 12

Thus, LCM(4, 6) = 12

Conclusion:

The LCM of 4 and 6 is 12, and it can be found using different methods such as prime factorization, listing multiples, and the division method.