LCM of 48, 72 and 92: How to find LCM of 48, 72 and 92?
The LCM of 48, 72 and 92 is 3312. Least Common Multiple (LCM) of a group of numbers is the smallest number that all of them can fit into. In this blog, we’ll explain easy ways to find the LCM of 48, 72, and 92.
Methods to find the LCM of 48, 72, and 92
Here are three simple methods to find the LCM of 48, 72, and 92:
1. Prime Factorization Method
Break each number into its prime factors and use the highest power of each factor.
- 48 = 2 × 2 × 2 × 2 × 3 (or 2⁴ × 3)
- 72 = 2 × 2 × 2 × 3 × 3 (or 2³ × 3²)
- 92 = 2 × 2 × 23 (or 2² × 23)
- Taking the highest powers: 2⁴ × 3² × 23 = 3312
Thus, LCM(48, 72, 92) = 3312.
2. Listing Multiples Method
List the multiples of each number and find the smallest one they all share.
- Multiples of 48: 48, 96, 144, 192, 240, 288, ..., 3216, 3264, 3312, ...
- Multiples of 72: 72, 144, 216, 288, 360, ..., 3168, 3240, 3312, ...
- Multiples of 92: 92, 184, 276, 368, 460, ..., 3128, 3220, 3312, ...
- The smallest common multiple is 3312.
Thus, LCM(48, 72, 92) = 3312.
3. Division Method
Divide all numbers by common factors until at least 2 numbers are divisible.
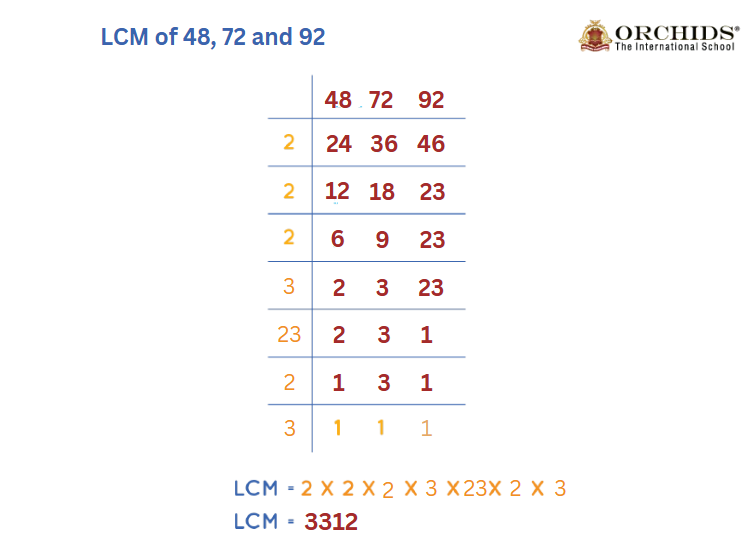
- Divide 48, 72, and 92 by 2 → (24, 36, 46)
- Divide 24, 36, and 46 by 2 → (12, 18, 23)
- Divide 12, 18 by 3 → (4, 6, 23)
- Divide 4, 6, and 9 by 2 → (2, 3, 23)
- 2, 3 and 23 are divisible by 1 only
- Multiply the divisors: 2 × 2 × 2 × 2 × 3 × 3 × 23 = 3312
Thus, LCM(48, 72, 92) = 3312.
Know how to find the lcm of 4 and 6 here.
Conclusion:
The LCM of 48, 72, and 92 is 3312, and you can find it using prime factorization, listing multiples, or division.
FAQs
-
What is the Least Common Multiple (LCM) of 48, 72, and 92?
The LCM of 48, 72, and 92 is 3312. This is the smallest number that is a multiple of all three numbers. You can find it by determining the prime factors of each number and then multiplying the highest powers of all prime factors present. -
How to Find the LCM of 48, 72, and 92 Using Prime Factorization?
To find the LCM using prime factorization:
-
Prime factors of 48: 2⁴ × 3
-
Prime factors of 72: 2³ × 3²
-
Prime factors of 92: 2² × 23
Take the highest powers of all prime factors: 2⁴, 3², and 23. Multiply them together: 2⁴ × 3² × 23 = 3312.
-
What Are the Methods to Find the LCM of 48, 72, and 92?
Common methods include:
-
Prime Factorization: Break down each number into prime factors and multiply the highest powers of all primes.
-
Division Method: Divide the numbers by common prime factors until all results are 1, then multiply the divisors.
-
Listing Multiples: List multiples of each number and identify the smallest common multiple.











