Angle Definition
Introduction to Angle Definition
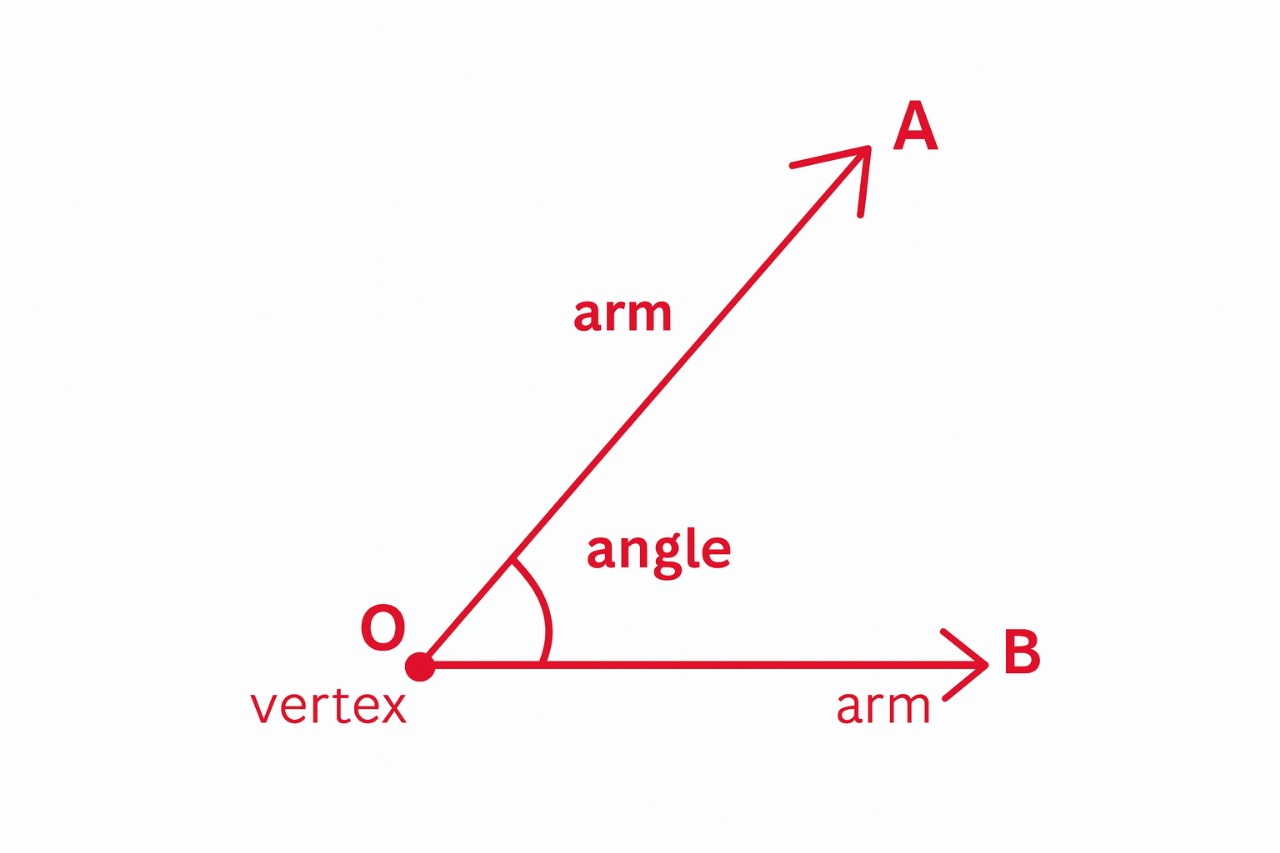
In mathematics, an angle is formed when two straight lines meet at some point. This point is called the vertex of the angle, and the two lines are called the arms of the angle.
For example, if you open a book a little, two sides form an angle in the corner where they are involved. Angles help us measure how much something has turned or opened. They are measured in degrees (°). A small angle means a small opening, and a big angle means a wide opening. So, an angle is simply the space between two lines that meet at a common point.
Table of Contents
- Angle Definition
- Types of Angles
- Properties of Angles
- Examples of Angles in Real Life
- Solved Examples
- Conclusion
- FAQs on Angle Definition
Angle Definition
In maths, an angle is a shape made when 2 lines or rays meet at 1 point. This meeting point is called the vertex, and the 2 lines are called the sides of the angle. The word angle comes from the Latin word “angulus”, which means corner.
Angles are shown using a symbol ∠. To write the size of an angle, we often use letters like θ (theta), α (alpha), β (beta), and so on.
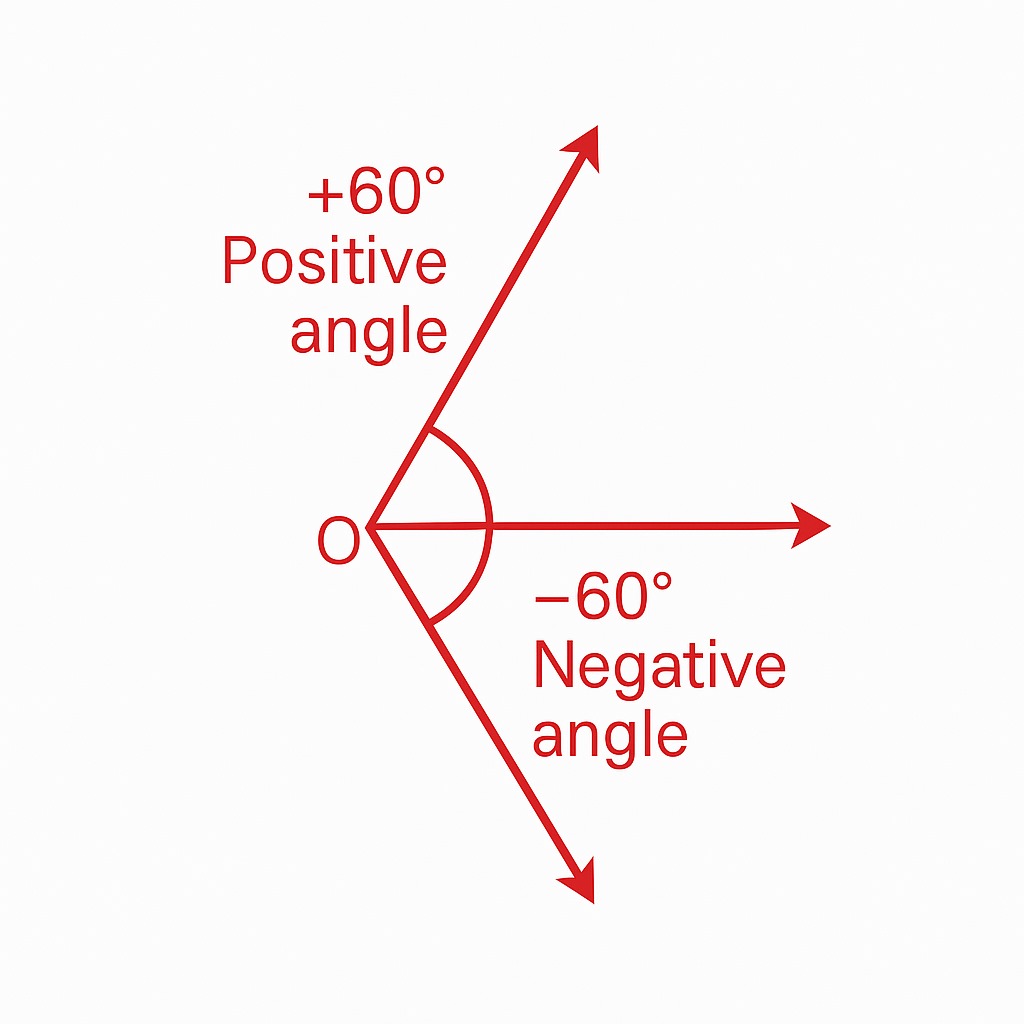
Positive and Negative Angles
When you measure an angle, you need to see in which direction it is turning:
-
Positive Angle: If the angle is measured anticlockwise
-
Negative Angle: If the angle is measured clockwise.
How to name an angle?
There are 2 main ways to name an angle:
-
Using One Letter
-
If there is only one angle at a point, we can name it with a single letter.
-
Example: If the angle is at point A, we write it as ∠A.
-
Sometimes we also use small letters like ∠x or symbols like ∠θ.
-
Using Three Letters:
-
If there are many angles at the same point, we use 3 letters.
-
The middle letter is always the vertex.
-
Example: In triangle ABC, the angle at A can be written as ∠BAC or ∠CAB. If it is 60°, we write ∠BAC = 60°
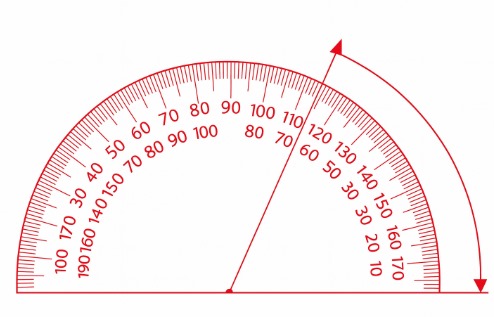
How to Measure an Angle?
Angles are measured in degrees (°).To measure angles, we use a tool called a protractor.
-
A protractor is a half-circle marked with numbers.
-
It has 2 sets of numbers
-
One goes from 0° to 180° on the outer side.
-
The other goes from 180° to 0° on the inner side.
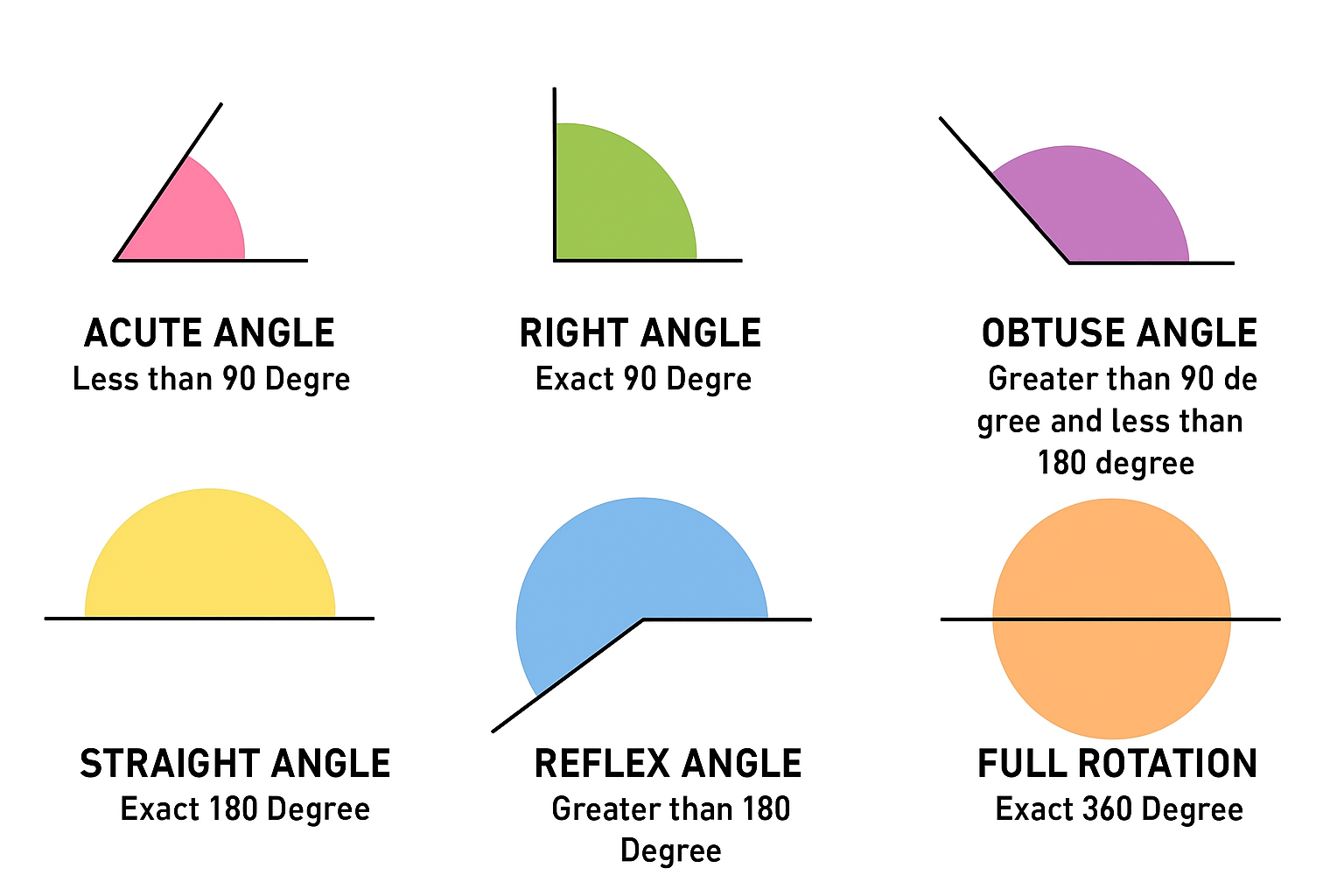
Types of Angles
Angles are an important part of geometry. They are formed when 2 lines or rays meet at a point. We can divide angles into different types depending on how big they are & how they are formed with lines. Types of angles based on measurement:
-
Acute Angle: An angle that is smaller than 90°. Example: 30°,45°,80°
-
Right Angle: An angle that is exactly 90°, it looks like the corner of a square.
-
Obtuse Angle: An angle that is bigger than 90° but smaller than 180°. Example:120°,130°.
-
Straight Angle: An angle that is exactly 180°, which looks like a straight line.
-
Reflex Angle: An angle that is bigger than 180° but smaller than 360°. Example:220°, 300°.
-
Full Angle: An angle that is exactly 360°, it is a full turn around a point.
Angles Formed by Lines and Transversals
When two or more lines are cut by another line, many angles are formed. These angels are given special names depending on their position on the lines. The lines can be either parallel or not, but when they are parallel, special rules apply.
Common Types of Angle Pairs:
-
Corresponding Angle: These angles are in the same position on each line. And they are always equal when the lines are parallel.
-
Alternate Interior Angles: These angles are on the inside of the 2 lines but on opposite sides of the transversal. When the lines are parallel, these angles are always equal.
-
Alternate Exterior Angles: These angles are the outside of 2 lines but on opposite sides of the transversal. When the lines are parallel, these angles are also equal.
-
Interior Angles on the Same Side of the Transversal: These angles are on the inside of the two lines & the same side of the transversal. When the lines are parallel, these two angles add up to 180°.
-
Supplementary Angles: Two angles are called supplementary if their sum is 180°. They don’t have to be on parallel lines.
-
Adjacent Angles: Two angles are adjacent if they are next to each other & share a common side & vertex.
-
Vertical Angles: When two lines cross each other, they form angles opposite to each other. These opposite angles are always equal, even if the lines are not parallel.
Important Angle Rules(Theorems):
When 2 parallel lines are cut by a transversal, the following rules always apply:
-
Alternate interior angle, alternate exterior angle, and corresponding angle are equal.
-
Interior angles on the same side of the transversal add up to 180°.
-
Vertical angles are always equal, even if the lines are not parallel.
Properties of Angles
-
Angles on a straight line: The sum of angles on a straight line is always 180°.
-
Angles around a point: The sum of angles around a point is always 360°.
Examples of Angles in Real Life
Here are real-life applications of different types of angles in geometry:
-
Clock hands: The angle between the hour and minute hands shows different types of angles, such as acute, obtuse, or even straight angles.
-
Road signs: Triangular and angular shapes in traffic signals show angles in degrees.
-
Books and doors: when half open, show the right angles and reflective angles.
-
Yoga and gymnastics: movement & pose form angles in a triangle, complementary and supplementary angles in a triangle, etc.
Solved Examples
Problem 1: Measuring Angles with a Protractor
Question: Use a protractor to measure the angle formed by two rays. The base ray lies along the 0° mark, and the second ray crosses the 70° mark.
Solution:
-
Place the vertex of the angle at the center of the protractor.
-
Align one arm along the 0° baseline.
-
Read the scale where the second ray crosses → 70°.
-
The angle measures 70°, which is an acute angle.
Concepts used:
-
The vertex and arms of an angle
-
Measuring angles with a protractor
-
Angle in degrees
-
Classification of angles (Acute)
Problem 2: Finding Unknown Angles Using Properties
Question: In a triangle, two interior angles are 65° and 45°. Find the third angle.
Solution:
-
Use the angle sum property of a triangle:
Sum = 180° -
Add the known angles: 65° + 45° = 110°
-
Subtract from 180°: 180° – 110° = 70°
-
The third angle is 70°, an acute angle.
Concepts used:
-
Angle in a triangle
-
Angle sum property
-
Classification of angles
-
Angle in degrees
Conclusion
Angles are made when 2 lines meet. They help us to measure the turns & shapes, we learned different types of angles, how to measure them, & how they appear in real life, like in clocks, doors, and road signs. Knowing angles makes both math and daily life easier to understand.
FAQs on Angle Definition
1. What is the simple definition of angle?
Ans: In-Plane Geometry, a figure that is formed by two rays or lines that share a common endpoint is called an angle. The word “angle” is derived from the Latin word “angulus”, which means “corner”.
2. What is an angle called?
Ans: There are four main types of angles: right angles, acute angles, obtuse angles, and straight angles. Right angles are like corners and measure 90°. Acute angles are smaller than 90°. Obtuse angles are larger than 90° but less than 180°.
3. Why are they called angles?
Ans: The name of the Angles may have been first recorded in Latinised form, as Anglii, in the Germania of Tacitus. It is thought to derive from the name of the area they originally inhabited, the Angeln peninsula, which is on the Baltic Sea coast of Schleswig-Holstein.
4. What does 360 angle mean?
Ans: A 360-degree angle is a complete angle or a full angle. It represents a complete rotation and represents a circle at a given point. In simple words, a circle has an angle of 360 degrees around the center. To form a 360-degree angle, the initial arm takes a full rotation and comes back to its original position.
5. What are the 12 types of angles?
Ans: There are several ways to categorize angles. Focusing on their measurement, there are six primary types: zero, acute, right, obtuse, straight, and reflex. Additionally, angle pairs like complementary, supplementary, vertical, and adjacent angles are also commonly discussed. Finally, angles can be classified as interior or exterior based on their position relative to a shape.
Related Links
CBSE Schools In Popular Cities
- CBSE Schools in Bangalore
- CBSE Schools in Mumbai
- CBSE Schools in Pune
- CBSE Schools in Hyderabad
- CBSE Schools in Chennai
- CBSE Schools in Gurgaon
- CBSE Schools in Kolkata
- CBSE Schools in Indore
- CBSE Schools in Sonipat
- CBSE Schools in Delhi
- CBSE Schools in Rohtak
- CBSE Schools in Bhopal
- CBSE Schools in Aurangabad
- CBSE Schools in Jabalpur
- CBSE Schools in Jaipur
- CBSE Schools in Jodhpur
- CBSE Schools in Nagpur
- CBSE Schools in Ahmednagar
- CBSE School In Tumkur