Symmetry - Definition, Line of Symmetry, Types and Examples

Symmetry is a necessary concept in geometry that helps us learn balance, patterns, and shapes. In other words, symmetry means a mirror image of a shape or figure. When you fold the paper and both halves are similar, that imaginary line that separates equal halves is identified as a line of symmetry. Symmetry is also found in art, nature, design, etc. The butterfly is one of the best examples of symmetry.

Table of Contents

• What is Symmetry?
• Types of Symmetry
• Line of Symmetry
• Reflective Symmetry
• Rotational Symmetry
• Point Symmetry
• How to Identify Symmetrical Shapes?
• Examples of Symmetry in Everyday Life
• Conclusion and Summary
• FAQs on Symmetry
• Related Articles

What is Symmetry?

Symmetry is a geometrical concept that describes patterns in shapes and objects. A figure has one side that is a mirror image of another side and then it is said to be in symmetry. Imagine you draw an imaginary line that makes exactly half, that line is known as the line of symmetry. 

Observe the image below, which shows symmetry in the human face, in a mandala and in the Taj Mahal. 

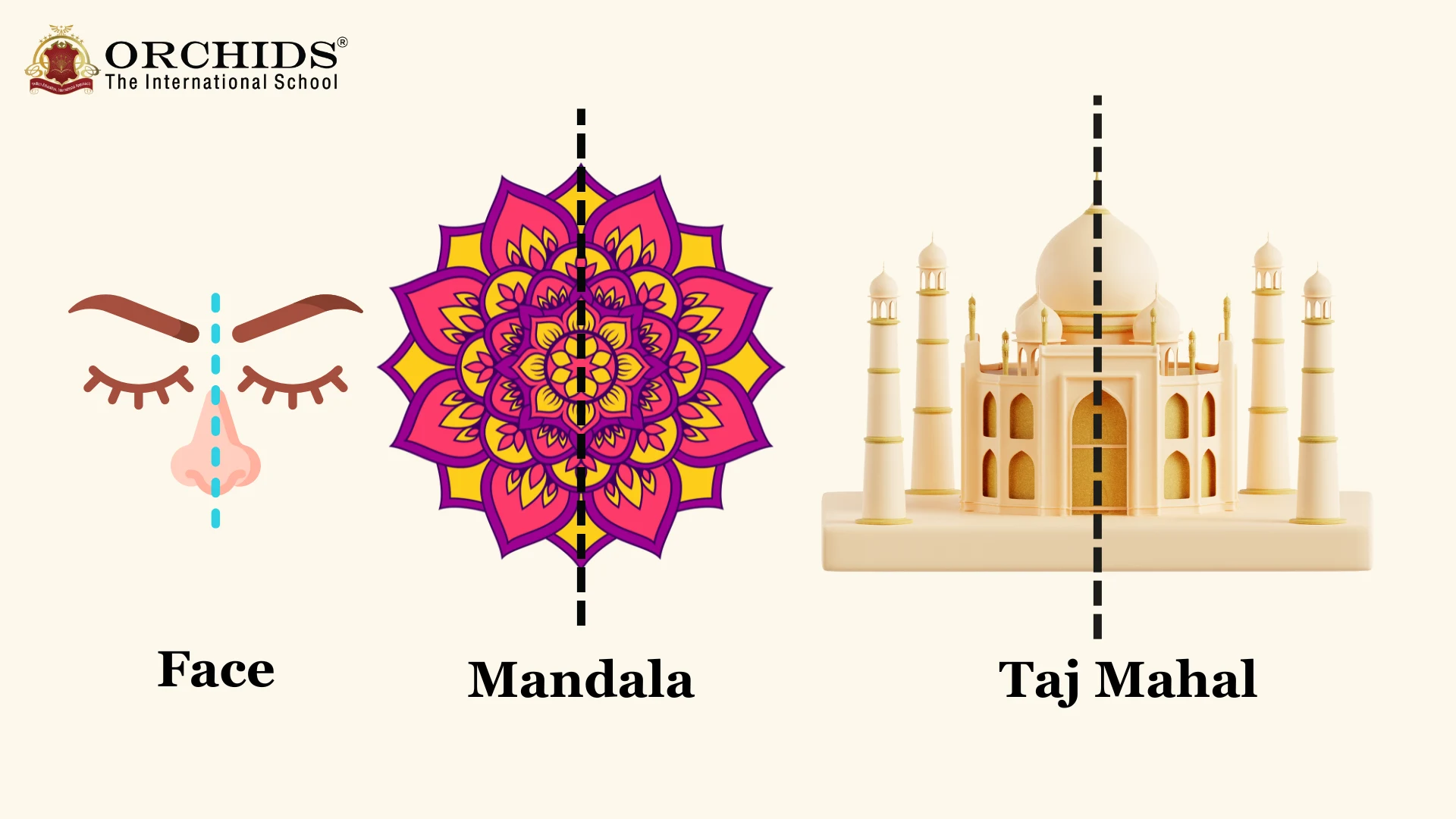
Types of Symmetry

Symmetry makes us understand the concept of patterns, designs and architectures. We can see symmetry in our nature, like in leaves, snowflakes and in some man-made architectures. The different types of symmetry are line of symmetry, reflective symmetry, rotational symmetry and point symmetry. 

Let us understand each type of symmetry briefly.

Line of Symmetry

A Line of Symmetry is an imaginary line that divides a shape into two identical halves. If you fold any figure along this line, both parts match exactly. This line of symmetry is also known as a mirror line. 

Most of the shapes in geometry have lines of symmetry. It can be one line of symmetry, two lines of symmetry, three lines of symmetry, or infinite lines of symmetry. Not only in shapes, we can also find a line of symmetry in objects, nature, arts, etc. 

Let us observe the image below that shows 1 line of symmetry, 3 lines of symmetry, 4 lines of symmetry and infinite lines of symmetry.

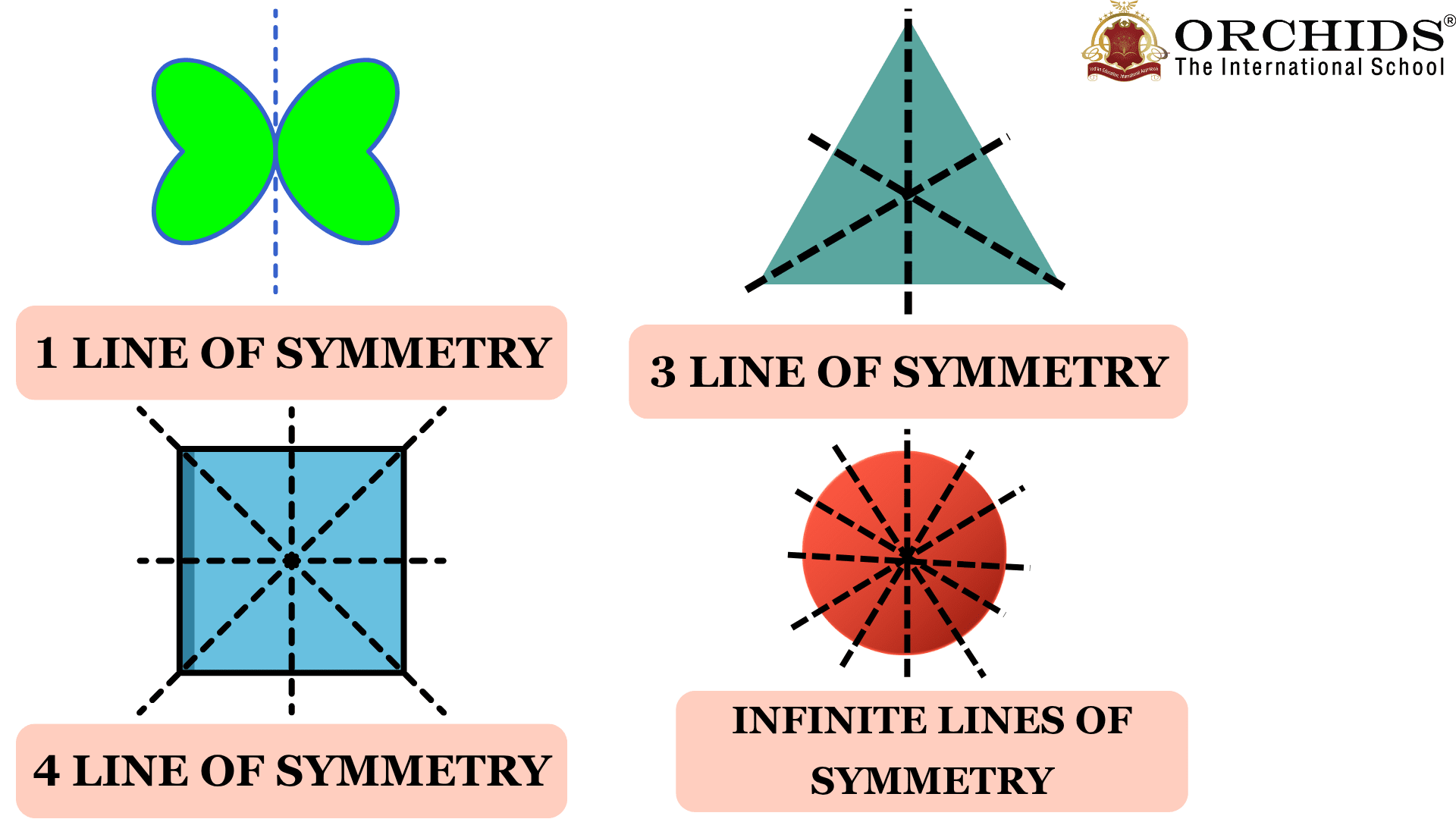
Examples:

• A rectangle has 2 lines of symmetry (vertical and horizontal).

• A heart shape has 1 vertical line of symmetry.

• Letters like A, M, and T have line symmetry, while letters like F or G do not.

Reflective Symmetry

Reflective Symmetry, which is also called mirror symmetry. This type of symmetry appears when one half of a figure is the mirror image of the other half. When the figure is divided by a line of reflection, reflective symmetry occurs. 

Reflective symmetry can be found in both nature and man-made designs. If a figure is said to have reflective symmetry, then each point on one side will have another matching point on the other side and also equidistant from the line. 

Examples:

• Leaves have reflective symmetry.

• When a pair of gloves lies side by side, it shows mirror symmetry.

• The English alphabets have reflective symmetry, like in letter A.

• Cathedral windows are designed symmetrically.

Rotational Symmetry

When an object is rotated in a particular direction and if it looks the same, then the object has Rotational Symmetry. It is also known as Radial Symmetry. During full rotation (360°), the number of times the shape matches with its original is called its order of rotational symmetry.

A shape is said to be in rotational symmetry if it looks the same after a certain degree of rotation, like 90°, 180°, or 120°.

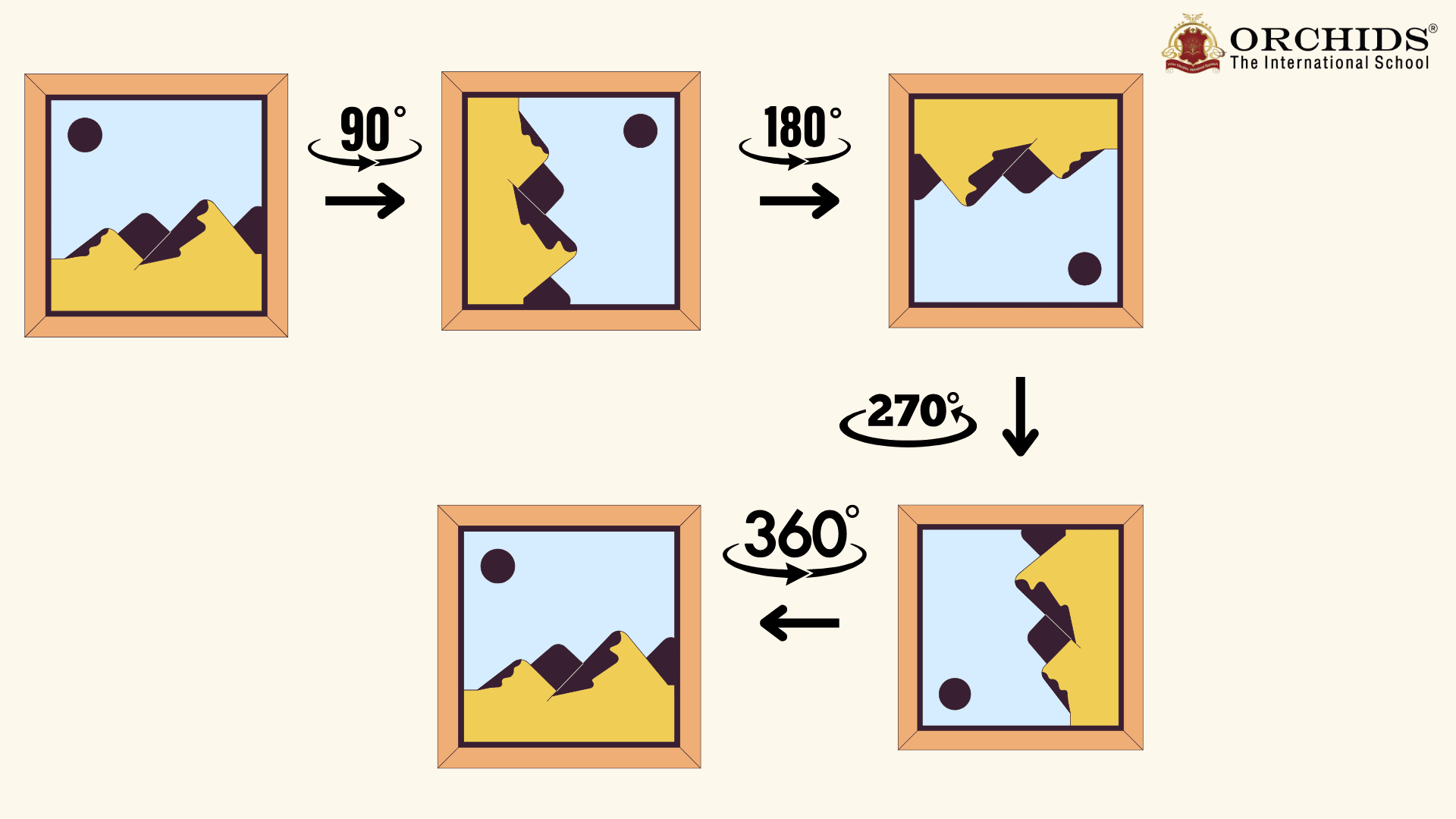
Examples:

• A square has rotational symmetry of order 4 (every 90°).

• An equilateral triangle has rotational symmetry of order 3 (every 120°).

• The letter “N” has rotational symmetry of order 2 (180°).

Point Symmetry

Point Symmetry appears in a shape from a central point to the matching part at an equal distance in the other direction. In simple terms, a shape is said to have point symmetry if it looks the same when it is rotated 180 degrees around a central point. 

In coordinate geometry, point symmetry is known as origin symmetry. 

Examples:

• The letter “S” has point symmetry.

• Most of the playing cards have point symmetry.

How to Identify Symmetrical Shapes?

• Draw an imaginary line that divides the shape into two identical halves: If both parts are equal, the shape has line symmetry.

• By rotating the shape: While rotating a full turn (360°) and if it looks the same after some rotation, it is said to have rotational symmetry.

• Identify the mirror image: When the mirror is placed along a line of symmetry and the other side looks exactly as the original, then the shape or object is symmetrical.

• A simple way to check is by folding the shape: If the shape or paper folds into equal halves, it’s symmetrical.

• Identify the symmetry in nature and man-made structures: You can easily identify the symmetry in man-made objects, like tiles, windows, buildings, etc.

Examples of Symmetry in Everyday Life

Symmetry can be found in many places. Observe the images below, where you can see symmetry in everyday life.

Conclusion and Summary

Learning symmetry helps us to learn more about patterns, designs, structures, etc. It can be seen in nature, architecture, human-made things and everyday life. By understanding different types of symmetry, such as line of symmetry, reflective symmetry, rotational symmetry and point symmetry, you can improve spatial thinking and problem-solving. Spot symmetry around you and keep revising for your improvement.

FAQs on Symmetry

1: What is symmetry in geometry?

Answer: A shape is said to be symmetrical when it is divided into two equal parts.

2: Write the types of Symmetry?

Answer: There are 4 main types of symmetry. They are:

1. Line of symmetry

2. Reflective symmetry

3. Rotational symmetry

4. Point symmetry.

3: How to find whether the shape is symmetrical? 

Answer: A simple way to know the symmetry in a shape is to fold or draw a line; the line that divides a shape into two identical parts is a line of symmetry.

4: How many lines of symmetry will there be in a shape?

Answer: There can be 1, 2, 3, 4, or infinite lines of symmetry in a shape.

5: Why is symmetry important in maths?

Answer: Symmetry helps understand patterns, improves spatial reasoning, and is useful in geometry, art, and design.

Related Articles

• Line of Symmetry

• Rotational Symmetry

• Reflective Symmetry

• Point Symmetry