Value of Log 1 to 10

The value of log 1 to 10 is a crucial concept in mathematics, particularly in algebra, logarithmic equations, and scientific applications. Understanding these log values helps simplify calculations and solve real-world problems in engineering, data analysis, and research. This guide explains what logarithms are, how to calculate log values, and provides the exact values of log 1 to 10 clearly and simply.

 

Table of Contents

• What is the Value of Log?
• What are Logarithms
• Value of Log 1 to 10 Table
• How to Calculate Log Value Manually
• How to Find the Value of Log Using a Calculator
• Logarithmic Properties You Should Know
• Misconceptions About Logarithms
• Solved Examples of Logarithmic Values
• Conclusion
• FAQs on Value of Log 1 to 10

 

 

What is the Value of Log?

When people ask, "What is the value of log?", they typically refer to base 10 logarithms.

Let’s apprehend it step-by-step:

• log₁₀(1) = 0 → because 100= 1000 = 1100=1

• log₁₀(10) = 1 → because a hundred and one=10101 = 10101=10

• log₁₀(a hundred) = 2 → because 102=100102 = 100102=100
  

The Value of logs relies on  matters:

• The base (maximum generally 10 or e),

• The quantity you're taking the log of.

Knowing the basic log values is crucial for fixing exponential and logarithmic problems effectively.

What are Logarithms

Logarithms are a mathematical concept that represent the opposite of exponentiation. In simple terms, a logarithm tells us the power to which a base must be raised to produce a given number. For example, since 10^3 = 1000, it means log₁₀(1000) = 3. The general form is written as logₑ(x) = y, which means b^y = x. The most common types are the common logarithm (base 10) and the natural logarithm (base e). Logarithms are useful for simplifying large calculations, solving exponential equations, and are widely used in science, engineering, computer science, and finance.

 

Value of Log 1 to 10 Table

This is a trendy reference desk of the value of log (base 10) from numbers 1 to 10. Memorising information that can simplify complicated math issues.

 

 These are rough values, typically rounded to four decimal places. This helps you use them when solving problems and understanding concepts on your own.

 

How to Calculate Log Value Manually

Many People ask, How to calculate log value manually? The top information is that there’s a technique:

Steps:

Break the number into recognised values or use the log of legal guidelines:

• log(ab) = log a + log b

• Log (a/b) = log a − log b

• log(aⁿ) = n × log a

Example:

“So, when learning to calculate log cost, remember the logarithmic laws. They help make simplification easier.”

 

How to Find the Value of Log Using a Calculator

Not everybody makes use of log tables anymore, so here’s the way to find the cost of the log of the usage of a scientific calculator:

• Press the LOG key.

• Type the wide variety (e.g., 7).

• Press = Enter.

• Your solution (e.g., log(7) = 0.8451) is displayed.

This is the quickest manner in case you're looking to discover the value of log for any range. Knowing the way to locate the cost of logging the use of tech equipment is a contemporary math skill.

 

Logarithmic Properties You Should Know

Understanding log properties helps you simplify and calculate the log price quickly. These are in particular useful for huge numbers or algebraic expressions.

Key Logarithmic Rules:

• logₐ(1) =0

• logₐ(a) = 1

• log(ab) = log a + log b

• Log (a/b) = log a − log b

• log(aⁿ) = n log a

Change of Base Formula:

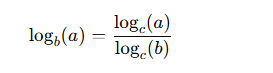
Mastering those allows you to understand how to calculate the log cost for unfamiliar numbers.

 

 

Misconceptions About Logarithms

There are numerous myths about logarithms that lead to confusion among People. Let’s explore and clarify them separately:

1 .Myth: log(1) = 1

Fact: log(1) = 0

Many students think that the log of 1 is 1; however, that’s incorrect. In reality, any quantity raised to the power of 0 equals 1, so the logarithm of 1 (in any base) is always zero.

 

2. Myth: log(ab) = log a × log b

Fact: log(ab) = log a + log b

This mistake comes from complicated logarithmic policies with algebraic multiplication. Logarithms flip multiplication into addition, making calculations less difficult. So, multiplying inside the log will become including outside.

 

3. Myth: You can locate the log of poor numbers

Fact: Logarithms of bad numbers are undefined in real numbers

Logarithms can only be taken for super numbers in real math. Since no actual strength of a wonderful range gives a poor result, the log of a poor quantity is undefined unless you are operating in complex numbers.

 

4. Myth: Logarithms are outdated

Fact: Logs are widely used in computing, device getting to know, and data

Some consider logs are handiest from antique math textbooks, however, that’s a long way from true. Logarithmic functions are vital in current programs like fact technology, AI models, algorithm complexity, and exponential statistics analysis.

 

Solved Examples of Logarithmic Values

Let’s apply what you’ve discovered in real examples:

 

Example 1: Find log(100)
 

Step 1: 100 = 10210^2102
Step 2: log(100) = log(10210^2102) = 2·log(10) = 2·1
Final answer: log(100) = 2

 

Example 2: What is the value of log(5)?
 

Step 1: Write 5 as 10/2 → log(5) = log(10/2)
Step 2: Use quotient rule → log(10/2) = log(10) − log(2)
Step 3: log(10) = 1 and log(2) ≈ 0.301030
Step 4: 1 − 0.301030 = 0.698970
Final answer: log(5) ≈ 0.698970

 

Example 3: Calculate log(9)
 

Step 1: 9 = 323^232
Step 2: log(9) = log(323^232) = 2·log(3)
Step 3: log(3) ≈ 0.477121 → 2 × 0.477121 = 0.954243
Final answer: log(9) ≈ 0.954243

 

Example 4: How to find the value of log(8)?
 

Step 1: 8 = 232^323
Step 2: log(8) = log(232^323) = 3·log(2)
Step 3: log(2) ≈ 0.301030 → 3 × 0.301030 = 0.903090
Final answer: log(8) ≈ 0.903090

 

Example 5: Find log(2 × 5) 

Method A (product rule): log(2×5) = log(2) + log(5) = 0.301030 + 0.698970 = 1.000000
Method B (recognize product): 2×5 = 10 → log(10) = 1
Final answer: log(2×5) = 1

These show not just what's the value of log, but additionally the way to calculate log cost the usage of rules and acknowledged values.

 

Conclusion

Logarithms may seem intimidating at the beginning; however, after you recognise the value of log 1 to 10, they become a lot less complicated to comprehend. From fixing simple math troubles to deciphering complex actual-global information, logarithms play an important role in many areas of getting to know and era. The price of a log allows us to make sense of exponential relationships, which are common in subjects like technology, engineering, and finance. By knowing the value of log for numbers 1 to 10, you build a solid basis for operating with logarithmic expressions. Learning how to calculate log value, the use of formulas and shortcuts permits you to simplify tough troubles. Practising how to discover the cost of a log with tables and calculators improves each pace and accuracy. With consistent practice and focus on their actual-life applications, logarithms can end up considered one of your maximum powerful and reliable mathematical tools.

 

 

Frequently Asked Questions on Value of Log 1 to 10

1. What is the fee for a log?

Answer: The price of log (base 10) depends on the wide variety; as an example, log(10) = 1 and log(1) = 0.

 

2. How a lot is 1 log?

Answer: Log(10) = 1 in base 10, which means 10 raised to the power 1 equals 10.

 

3. How to calculate a log?

Answer: Use a calculator or log desk, or follow log regulations like log(ab) = log a + log b.

 

4. How to study a log?

Answer: Logarithms are expressed as “log base (b) of number (x),” written as log₍b₎(x).

 

Discover the value of log 1 to 10 with Orchids The International School and strengthen your math foundation today!