Orchids Logo
Admissions 2025-26
9-999-431-999info@orchids.edu.in
Login
Doubt Connect
Orchids Logo

Numbers Up To 4 Digits

Place Value and Face Value for Class 3 Math

This learning concept is about the 3-digit number and the introduction of a 4-digit number. Here students will learn how to write the 3-digit number in words, the place value and face value of 3-digit numbers and the difference between them. Also, they will get to know about their expanded form of math.

Table of Contents

  • Introduction to Numbers up to 4 Digits

  • How Many Two-Digit Numbers Are There?

  • Understanding Three-Digit Numbers

  • Writing Three-Digit Numbers in Words

  • Introduction to Four-Digit Numbers

  • What is Place Value and Face Value??

  • Expanded Form of Numbers

  • Importance of Zero in Numbers

  • How Many Hundredths Are in 1.44?

This concept is explained to class 3 students using examples, illustrations and concept maps. At the end of the page, two printable worksheets with solutions are attached for the students.

Download the worksheets and solutions to assess our knowledge of the concept.

Number is an arithmetic value used for representing the quantity and used in making calculations. The symbols that are used to denote the numbers are called numerals.

Numbers are of various kinds. We have a long list that includes cardinal numbers, ordinal numbers, etc.

  • Cardinal numbers define how many of something are there in a list such as one, five, ten etc.
  • Ordinal numbers explain the position of something in a list.

How Many Two-digit Numbers Are There?

  • The smallest two-digit is 10. In words it is written as ‘ten’. We represent ten through a block of 10 unit cubes.

block of 10 unit cubes

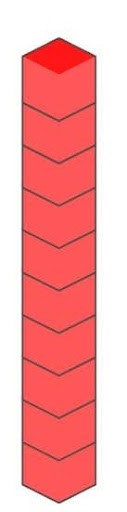
  • The Greatest two-digit number is 99. In words it is written as ‘Ninety-nine’.

99 can be represented by 9 ten blocks and 9 unit cubes as shown below.

99 blue blocks

If we add one more block with 99, then we get 100.

Easily we can count that there are 100 blocks of equal sizes.

So, 99 + 1 = 100

  • 100 is written in word as Hundred.

100 blue blocks

Three-digit Number

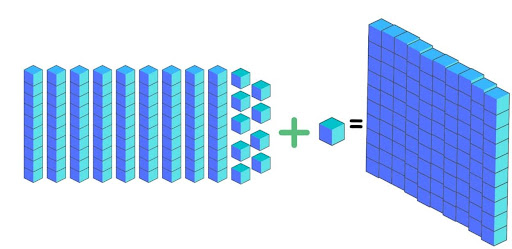
  • The smallest three-digit number is 100. We represent 100 through ten blocks of 10 as shown below.
ten blocks of 10
  • The greatest three-digit number is 999.

99 can be represented by 9 hundred blocks and 9 ten blocks.

99 can be represented by 9 hundred blocks and 9 ten blocks.
  • 999 in words is written as ‘Nine hundred and ninety-nine’.

Adding one smaller block with 999 results in 1000.

Adding one smaller block with 999 results in 1000

Easily we can count that there are 1000 blocks of equal sizes.

So, 999 + 1 = 1000

  • 1000 is written as ‘One Thousand’.

Write Three-Digit Numbers in Words

Here it is explained with an example.

Examples: Write these number in words:

(i)217     (ii) 408     (iii) 480     (iv) 699

Answer:

271

217 is written as Two hundred and seventeen.

408

408 is written as Four hundred and eight.

480

480 is written as Four hundred and eighty.

699

699 is written as Six hundred and ninety-nine.

4-Digit Number

Numbers up to 4 digits include all numbers from 0 to 9,999. That means we count from zero, then 1-digit numbers, then 2-digit numbers, then 3-digit numbers, and finally all the way to 4-digit numbers.

  • The number 7 is a small number with only one digit.

  • The number 35 is bigger because it has two digits.

  • The number 126 is even bigger with three digits.

  • And the number 3,482 is a big number with four digits.

The smallest four-digit number is 1000.

We represent 1000 through a cube of 10 ten-blocks.

1000 cube blocks
  • The greatest four-digit number is 9999.

What Is Place Value and Face Value?

Place Value of Numbers:

Place value is the value of each digit in a number.

  • To get the Place value of a digit in a number,
    1. Multiply the digit with 100, if the digit is in the hundred’s place
    2. Multiply the digit with 10, if the digit is in the ten’s place.
    3. Multiply the digit with 1, if the digit is in one’s place.

Here, it is explained with an example.

Examples: Write the place value of the digits in the numbers

a)368 b)108 c) 390

Answer:

  1. place value

The place value of 3 is 3 × 100 = 300.

The place value of 6 is 6 × 10 = 60.

The place value of 8 is 8 × 1 = 8.

  1. place value

The place value of 1 is 1 × 100 = 100.

The place value of 0 is 0 × 10 = 0.

The place value of 8 is 8 × 10 = 80.

  1. place value

The place value of 3 is 3 × 100 = 300.

The place value of 9 is 9 × 10 = 90.

The place value of 8 is 0 × 1 = 0.

Face Value of Numbers:

Face value is the actual value of a digit in a number.

Examples: Face value of the digit 6 in the number 634.

Answer:

6 is in the hundreds’ place.

Hence, the face value of the digit 6 in the number 634 is 6.

One should not confuse between the place value and the face value of a digit in a number.

Face Value of Numbers

Difference Between Place Value and Face Value:

Place Value Face Value
1) Place value represents a digit in a number according to its position in the number. 1)Face value is the actual value of a digit in a number
2)To get the place value of a number, we multiply the digit value with its numerical value. 2) The face value of a digit is the number itself.

Expanded Form Math

The number that is represented by the sum of each digit multiplied by its place value is called the expanded form of the number.

Here it is explained with an example.

Examples: Write the expanded form of the numbers

a) 789 b) 605

Example: a) 789 = 700 + 80 + 9

b) 605 = 600 + 0 + 5

Why Is Zero Important?

Zero helps us keep the right place for digits.

Example: 1,005

  • The zeros mean no hundreds or tens, but they hold the places so 1 is in thousands and 5 is in ones.

 

How Many Hundredths Are in 1.44?

Now, here’s a fun question: how many hundredths are in 1.44?

1.44 means 1 whole and 44 hundredths.

  • 1 whole = 100 hundredths

  • 0.44 = 44 hundredths

So, 1.44 = 144 hundredths!

Common Misconceptions

  1.  Thinking the face value and place value are always the same.
    Truth: Face value is the digit itself, but place value depends on its position. For example, in 506, the face value of 5 is 5, but its place value is 500.

  2.  Believing zero has no value.
    Truth: Zero holds place value and helps us keep digits in the correct position, like in 1,005.

  3.  Reading numbers from right to left instead of left to right.
    Truth: Always start reading numbers from the left (thousands, hundreds, tens, then ones).

 

 

Fun Facts

  • The biggest 4-digit number is 9,999 — that’s almost ten thousand!

  • Zero was invented more than 1,500 years ago to help with place values and math.

  • Place value helps computers understand numbers, just like it helps you!

  • 1.44 can be written as 144 hundredths, showing how decimals and fractions are related.

Numbers
 

FAQ’S

1. What is a 4-digit number in Class 3?

  • A 4-digit number is a number that has four digits — it starts from 1000 and goes up to 9999.

  • It is the smallest number that has a thousand's place.

  • Example places: Thousands, Hundreds, Tens, and Ones

2. What is an example of a 4-digit number?

  • Some examples of 4-digit numbers are:

    1000, 2345, 6789, 9999

  • All these numbers have four digits and are between 1000 and 9999

3. How many numbers are 4 digits?

  • There are 9000 four-digit numbers in total.

  • The smallest 4-digit number is 1000

  • The largest 4-digit number is 9999

So, total = 9999 − 1000 + 1 = 900

4. How many 4-digit numbers are there between 1000 and 3000?

  • We count all 4-digit numbers from 1000 to 2999.

  • First number = 1000

  • Last number = 2999

So, total = 2999 − 1000 + 1 = 2000 four-digit numbers

Share
Loading Footer...